The Fibonacci sequence is a collection of numbers where a number is the sum of the previous two terms. Fibonacci sequence always starts from 0 and 1:
Finding the Fibonacci number at the nth term using recursion is one of the most common coding interview problems that you may find, so let’s see how you can solve it in JavaScript.
The key to solving this coding problem is to use its mathematical formula and implement it in your recursive function. The mathematical formula to find the Fibonacci sequence number at a specific term is as follows:
Fn = Fn-1 + Fn-2
There are three steps you need to do in order to write a recursive function, they are:
- Creating a regular function with a base case that can be reached with its parameters
- Passing arguments into the function that immediately trigger the base case
- Passing a different, more complex arguments that trigger the recursive call just once.
For a Fibonacci sequence, the base case is that the zeroth and first number of the sequence are 0 and 1 respectively. You can write the base case in two ways:
if(n === 0) return 0;
if(n === 1) return 1;
Or you can write if (n < 2) return n because 0 + 1 equals to 1 anyway. Let’s start writing the function:
function fib(n) {
if (n < 2) {
return n;
}
}
The first step is done, and the second step is passing arguments into the function that will trigger the base case. You can do so by passing 1 into the function:
fib(1); // 1
All there’s left is to do the third step, which is passing arguments into the function that will trigger the recursive call at least once. Since the base case for the function is n < 2, this means you can trigger the recursive call once when you pass the number 2.
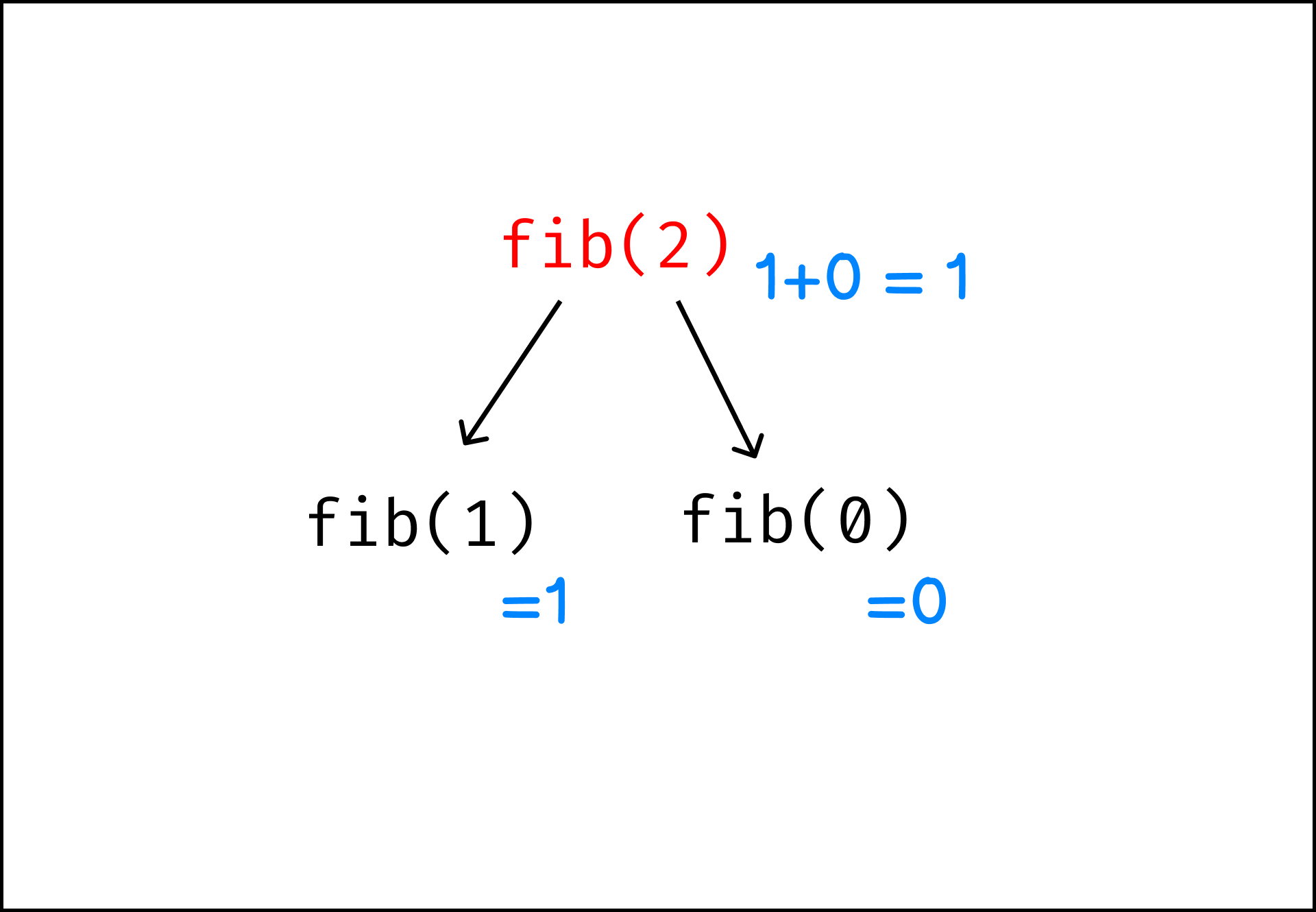
Here’s how a fib(2) call should resolve. Notice how the recursive call is following the formula:
Here’s how you write the recursive call to find the Fibonacci number at the nth term:
function fib(n) {
if (n < 2) {
return n;
}
return fib(n - 1) + fib(n - 2); // Fn-1 + Fn-2
}
To test your code, you simply need to call the fib function:
console.log(fib(3)); // 2
console.log(fib(5)); // 5
console.log(fib(8)); // 21
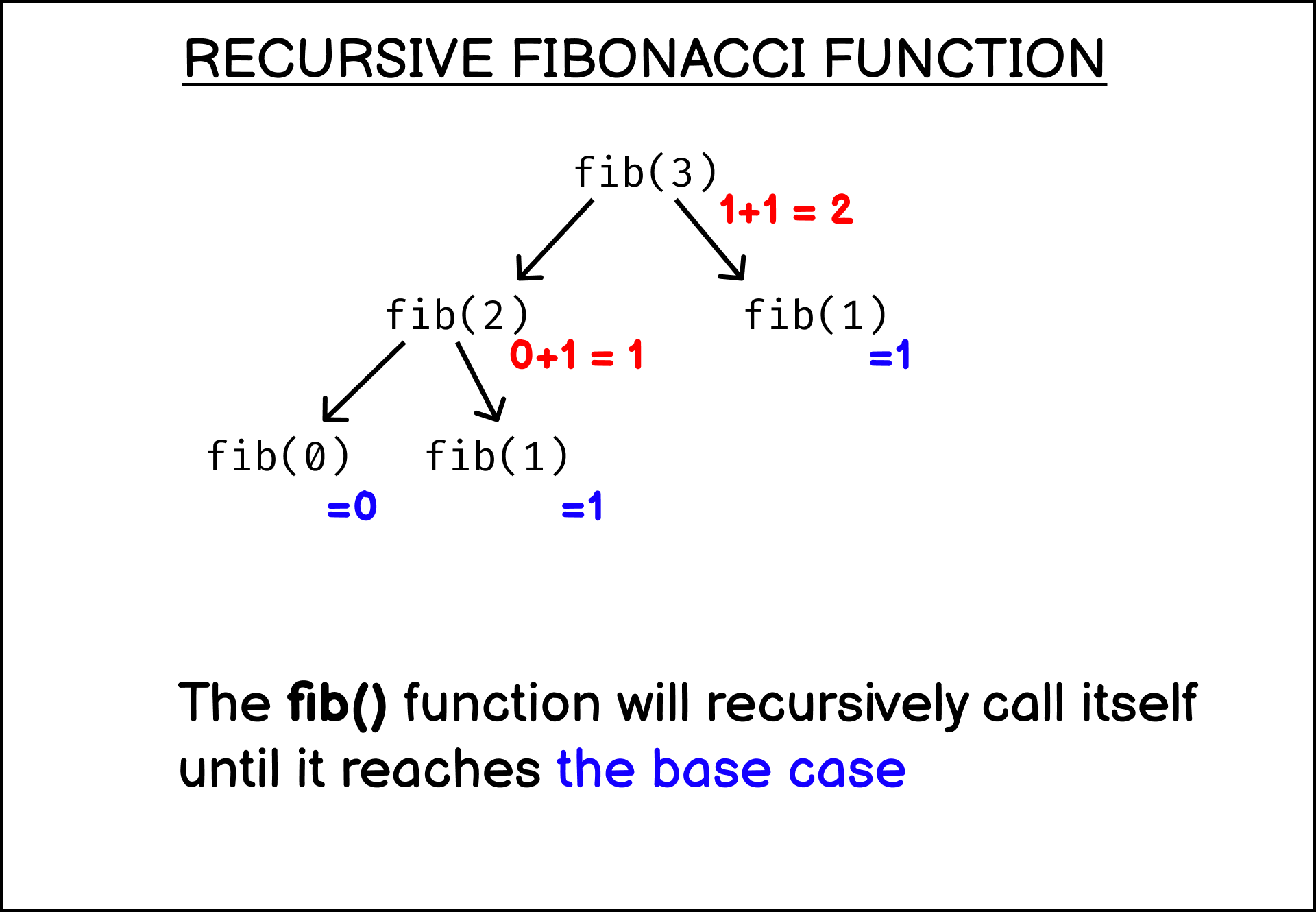
To drill the concept to your braind, here’s another illustration for fib(3) call in action:
You now have a working recursive Fibonacci function. Great job!
Optimizing recursive Fibonacci function performance with memoization
Although the recursive function above is working just fine, you can still improve its performance by using memoization. Memoization is simply an optimization technique used to speed up computer programs execution by storing the result of previous function calls.
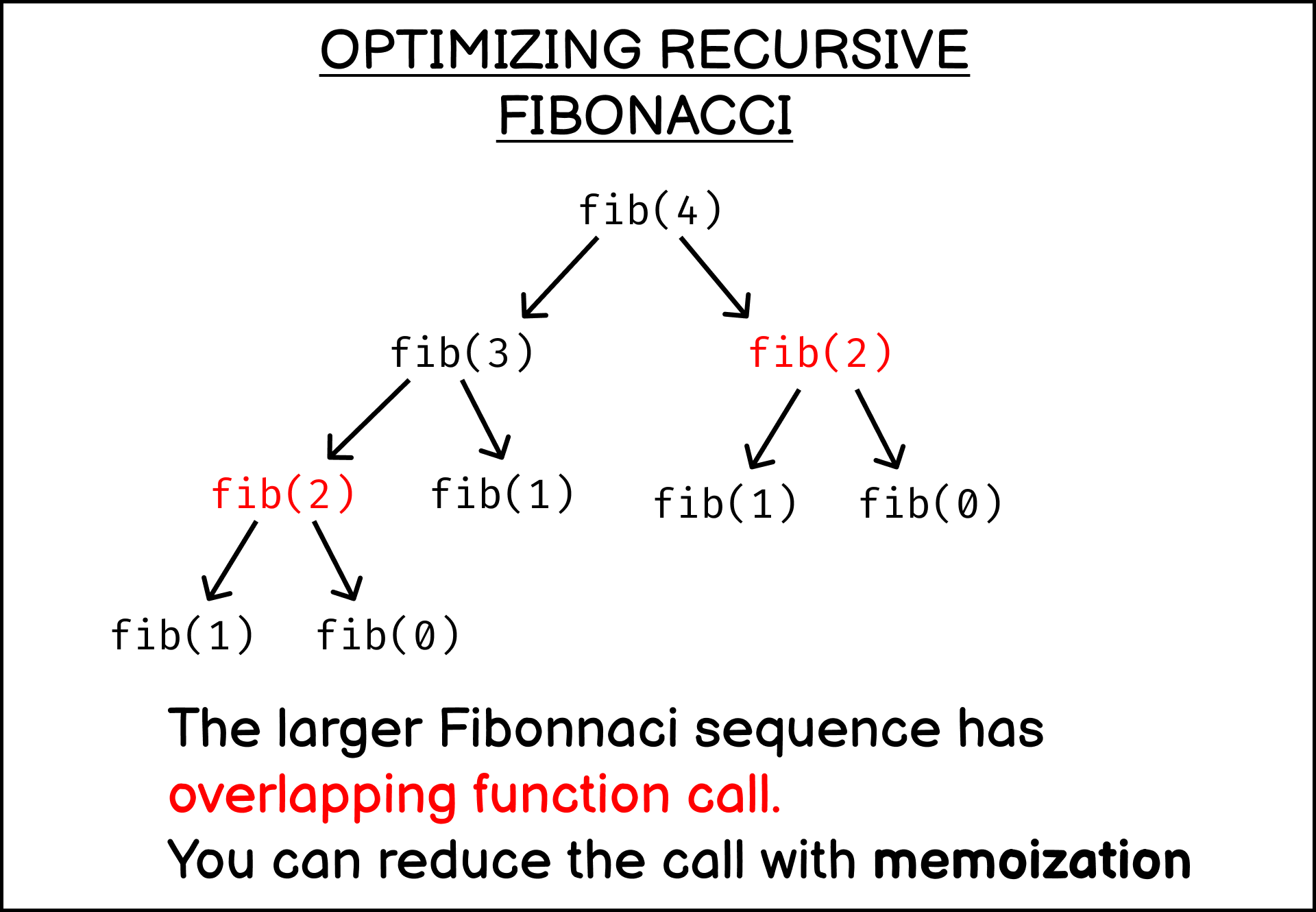
To understand how memoization works, let’s consider the following fib(4) execution example:
From the illustration above, you can see how fib(2) is called both in fib(4) and fib(3) execution even though it will return the same result. By using memoization, you can store the result of fib(2) call the first time it was executed so that the next call can simply retrieve it.
The easiest way to implement a memoization in JavaScript is by using an empty object ({}). First, you need to store the result of fib(n) call inside the object. The next time fib(n) is called, you just need to retrieve it from the object. Let’s call this object as memo:
function fib(n, memo) {
if (n < 2) {
return n;
}
if(!memo[n]) {
// when the object doesn't have the property of n
// store the result of the call inside memo[n]
memo[n] = fib(n - 1, memo) + fib(n - 2, memo);
}
return memo[n];
}
console.log(fib(5, {})); // 5
Following the illustration for fib(4) call, this means you retrieved the second fib(2) call from the memo object, which saves the function from calling fib(1) and fib(0) again. The number of recursive calls you reduce with memoization will increase as you call on the larger Fibonacci nth term.